説明

倍と割合Ⅱ

「倍と割合Ⅱ」は,「倍と割合Ⅰ」に続いて倍（割合）の概念を導き、その使い方と応用の習熟をはかることを目的とした教材です。「倍と割合Ⅰ」を学習する対象としては、「小数」「E」教材を学習し終えた子ども、つまり主として小学5年生を考えていましたが、「倍と割合Ⅱ」では、「F」教材の前半（分数の乗除）の内容を修得していることを前提としましたので、主として小学校6年生を対象に考えています。

各節の解説

「倍と割合Ⅰ」の前文で述べたように、倍はある量や数を同種の量や数に変える働きです。倍（割合）は日常生活においてもよく使われておりますので、各セクションにわたってできるだけ実際的な問題を取り上げ、倍（割合）が自由に使えるように配慮しました。

§1　倍

ブラックボックスを使って分数倍を導きます。整数倍,小数倍については「倍と割合Ⅰ」で扱っていますので、ここでは入力、出力、働き(倍)のいずれかが分数であるものについて、入力、働きを与えて出力を求める問題を扱います。

§2　倍を使う1

「倍と割合Ⅰ」の前文で述べましたように,入力,倍、出力の関係から、次の倍の3用法が成り立ちます。

第1用法　入力と出力がわかって,倍を求める。

第2用法入力と倍がわかって、出力を求める。

第3用法出力と倍がわかって,入力を求める。

• 入力と倍(割合)がわかって、出力を求める。(4)
• 入力と出力がわかって,倍(割合)を求める。(5～6)
• 出力と倍(割合)がわかって,入力を求める。(7～8)
• 4～8のまとめの問題を扱う。(9)

§3　倍を使う2

倍(割合)を使う加法的複合問題を扱います。

• 入力の(p+α)倍を求める。(10)
• 入力の(1±p)倍を求める。(11～14)
• 入力を求める。(15～16)
• 割合の応用として食塩水の問題を扱う。(17)

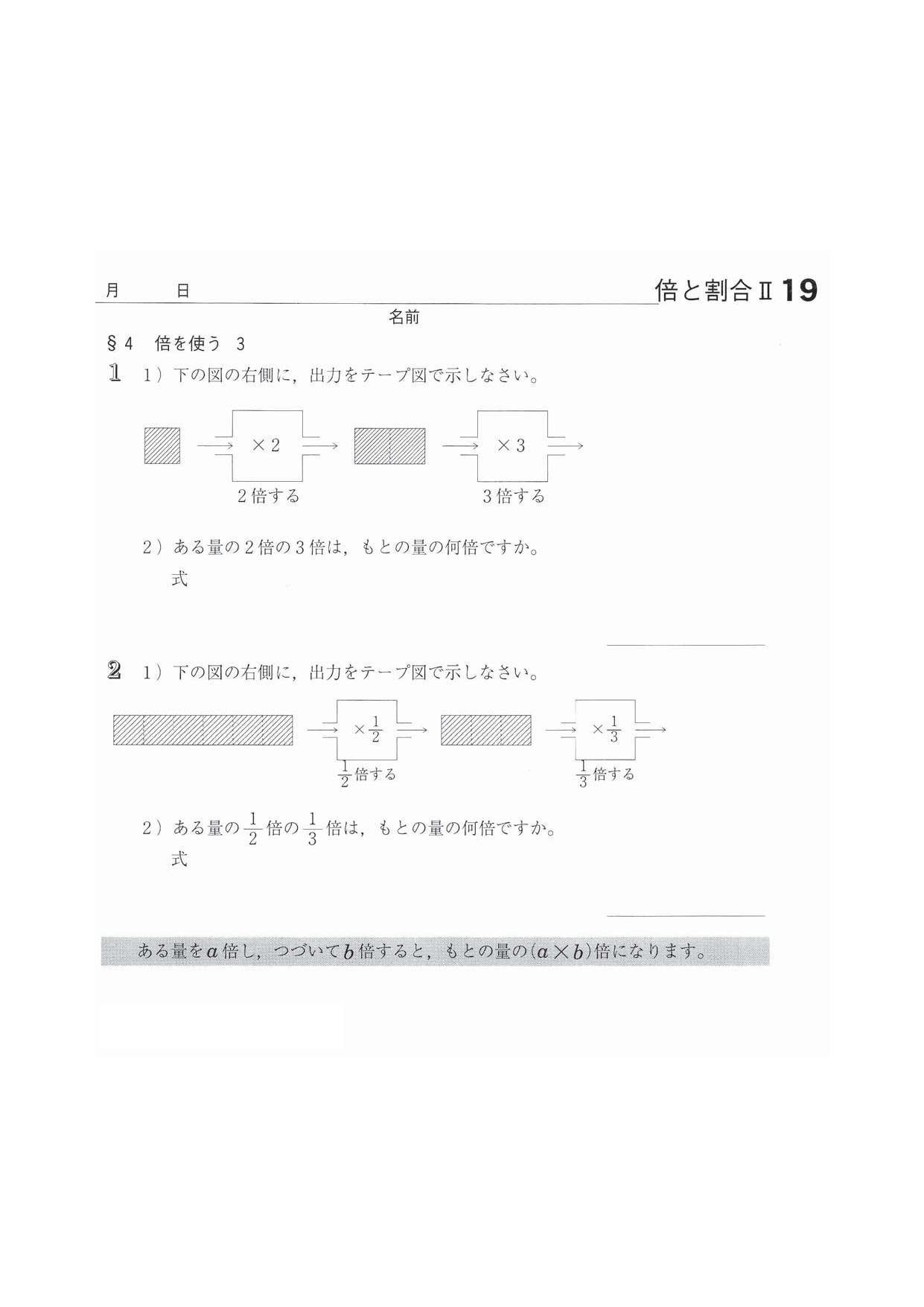
§4　倍を使う3

倍(割合)を使う乗法的複合問題を扱います。
ある量xのP倍のq倍はもとの量xの(p×g)倍に等しく、これを式で表すと、(x×p)×q=x×(p×g)となります。

• ○入力のp×q倍を求める。(18～20)
• ○出力、倍(割合)、入力を求める。(21,22～24)

※7番以降は、本商品には含まれませんので、別途お買い求め下さい。
※解答書は、解答書のページをご参照下さい。